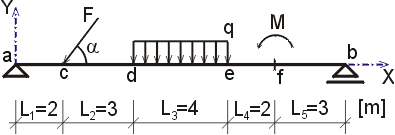
Dané: F = 20 kN, cosa = 0.6, sina = 0.8, q = 6 kN/m, M = 18 kNm.
Prostý nosník - ilustračný príklad - detailné riešenie

|
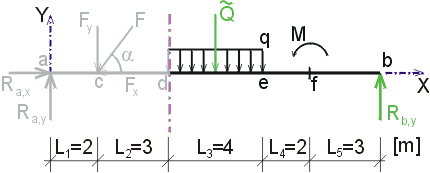
Určte reakcie a priebehy vnútorných síl na zadanom prostom nosníku. Dané: F = 20 kN, cosa = 0.6, sina = 0.8, q = 6 kN/m, M = 18 kNm. |
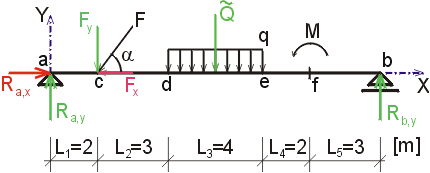 |
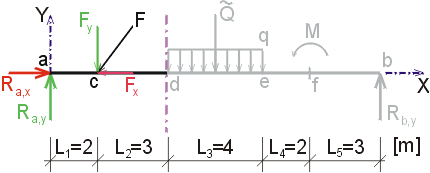
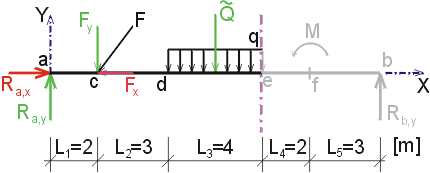
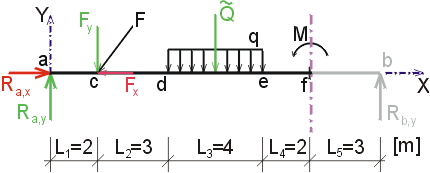
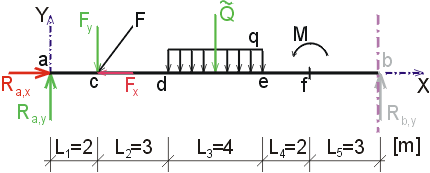
1) Výpočet reakciíNajskôr rozložíme silu F na vodorovnú zložku Fx a zvislú zložku Fy a spojité rovnomerné zaťaženie q medzi bodmi d,e nahradíme náhradným bremenom Q, ktoré pôsobí v ťažisku zaťažovacieho obrazca :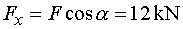 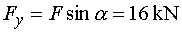 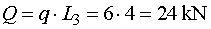 Teleso uvoľníme, tzn. nahradíme väzby (podpery) zložkami reakcií. Bod a je podoprený pevným neposuvným kĺbom. V tomto kĺbe vznikajú dve zložky reakcií - vodorovná zložka Ra,x a zvislá zložka Ra,y. Bod b je podoprený posuvným kĺbom, v ktorém vzniká iba jedna zložka reakcie - zvislá Rb,y. Veľkosť neznámych zložiek reakcií určíme z podmienok rovnováhy v tvare: 1) 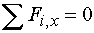 : :
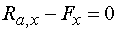 2) 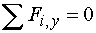 : :
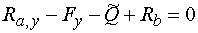 3) 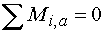 : :
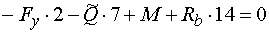 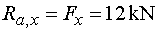 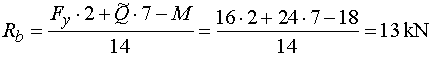 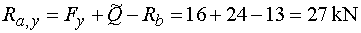 |
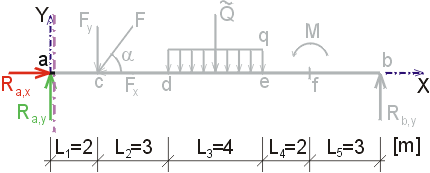 |
Na - vedieme rez v bode a tesne sprava.
Na myslene odrezanej časti pôsobí v smere osi x iba sila Ra,x.
Podľa konvencie o smere kladných normálových síl teda pôsobí záporne (pôsobí smerom do prierezu).
Teda platí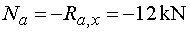 |
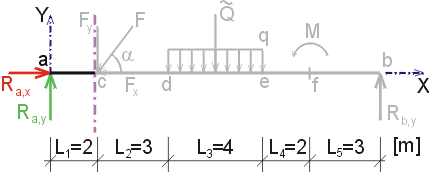 |
Ncl - vedieme rez v bode c tesne zľava.
To znamená, že na myslene odrezanej časti nosníka nepôsobí eště sila F.
V smere osi x teda pôsobí stále iba sila Ra,x.
Podľa konvencie pre smer kladných normálových síl pôsobí záporne (pôsobí smerom do prierezu).
Teda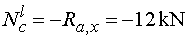 |
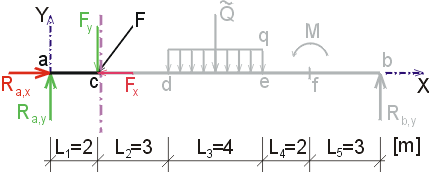 |
Ncp - vedieme rez v bode c tesne sprava.
To znamená, že na odrezanej časti nosníka už pôsobí aj sila F.
V smere osi x teda pôsobí iba reakcia Ra,x (záporne)
a vodorovná zložka Fx sily F pôsobiaca
podľa konvencie kladne (pôsobí von z prierezu). Teda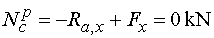 |
 |
Ndl - vedieme rez v bode d tesne zľava.
Na odrezanej časti nosníka pôsobí v smere osi x reakcia
Ra,x (záporne) a vodorovná zložka Fx (kladne).
Teda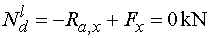 |
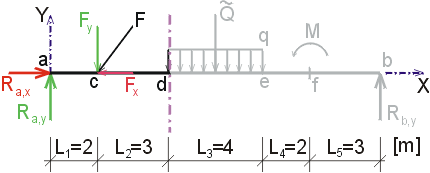 |
Ndp - vedieme rez v bode d tesne sprava.
Na odrezanej časti nosníka začíná pôsobiť spojité rovnomerné zaťaženie.
To však pôsobí v smere osi y, takže neovplyvní normálové sily.
V smere osi x teda pôsobí iba reakcia Ra,x (záporne)
a vodorovná zložka Fx (kladne).
Teda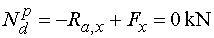 |
 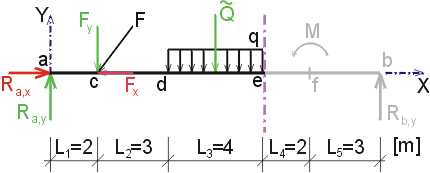 |
Nel, Nep
- ak vedieme rez v bode e tesne zľava alebo tesne sprava (teda na konci pôsobenia spojitého zaťaženia), vidíme, že
na odrezanej časti nosníka nepribudlo žiadne zaťaženie ve smere osi x, ktoré by vyvolalo zmenu veľkosti normálových síl.
V smere osi x teda pôsobí iba reakcia Ra,x (záporne)
a vodorovná zložka Fx (kladne).
Teda Nel = Nep
= Ne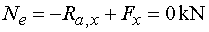 |
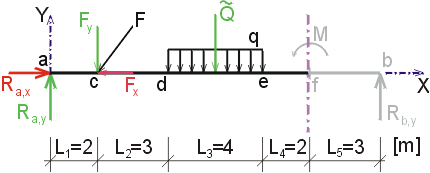  |
Nfl, Nfp
- ak vedieme rez v bode f tesne zľava alebo tesne sprava (teda pred miestom pôsobenia
osamelého momentu a za týmto miestom), vidíme, že moment neovplyvní normálové sily.
V smere osi x teda stále pôsobí len reakcia Ra,x (záporne)
a vodorovná zložka Fx (kladne).
Teda Nfl = Nfp
= Nf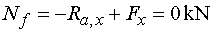 |
 |
Nb, ak určujeme normálovú silu v bode b, vedieme rez tesne zľava.
Na odrezanej časti stále pôsobí v smere osi x len reakcia Ra,x (záporne)
a vodorovná zložka Fx (kladne).
Teda 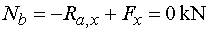 |
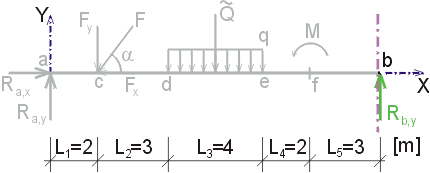 |
Nb - vedieme rez v bode b tesne zľava.
Na odrezanej časti nepôsobí v smere osi x žiadna sila.
Teda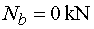 |
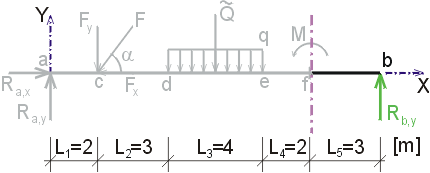 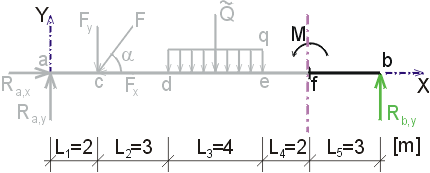 |
Nfp, Nfl
- ak vedieme rez v bode f tesne sprava alebo tesne zľava, zistíme, že
na odrezanej časti nepôsobí ani v jednom případe v smere osi x žiadna sila. Teda Nfp = Nfl = Nf 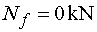 |
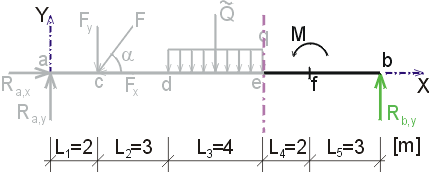 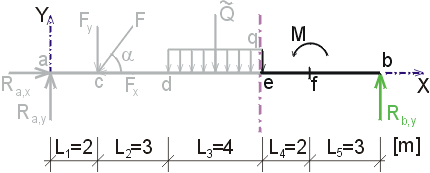 |
Nep, Nel
- ak vedieme rez v bode e tesne sprava alebo tesne zľava, dôjdeme
ke rovnakému záveru aako v predchádzajúcom prípadě - na odrezanej časti nepôsobí
ani v jednom prípade v smere osi x žiadna sila. Teda platí Nep = Nel = Ne 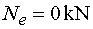 |
 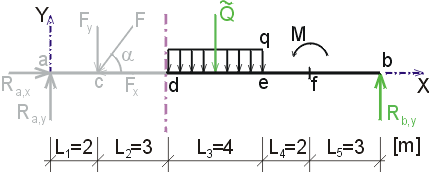 |
Ndp, Ndl
- ak vedieme rez v bode d tesne sprava alebo tesne zľava, zistíme, že
se opäť opakuje situácia z predchádzajúcich dvoch případov - na odrezanej časti nepôsobí
ani v jednom prípade vesmere osi x žiadna sila. Teda Ndp = Ndl = Nd 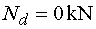 |
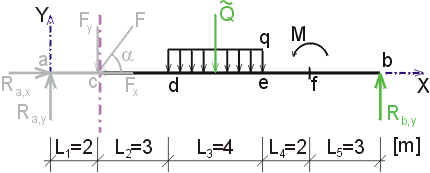 |
Ncp - ak vedieme rez v bode c tesne sprava,
t.j. tesne pred pôsobiskom sily F. Na odrezanej časti teda stále
ešte nepôsobí žiadna sila v smere osi x.
Teda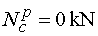 |
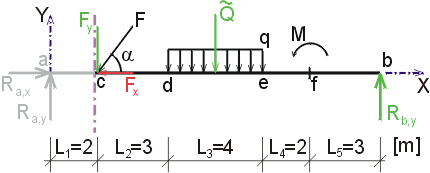 |
Ncl - ak vedieme rez v bode c tesne zľava,
t.j. tesne za pôsobiskom sily F. Na odrezanej časti teraz už pôsobí
zaťaženie v smere osi x, a to vodorovná zložka Fx.
Táto zložka pôsobí proti konvenci (pôsobí do prierezu), teda záporne.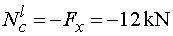 |
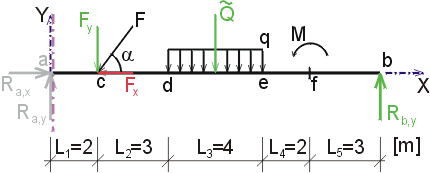 |
Na - ak vedieme rez v bode a tesne sprava, potom na odrezanej časti pôsobí
v smere osi x iba vodorovná zložka Fx (záporne).
Teda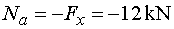 |
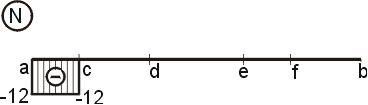
|
Ak máme vypočítané hodnoty normálových síl, môžeme nakresliť tzv. obrazec normálových sil (graf normálových sil, priebeh normálových sil). Ten vykreslíme tak, že na os nosníka vynesieme vypočítané hodnoty. Kladné hodnoty normálových sil vynášame nad os nosníka, záporné pod os nosníka. Vynesené body potom spojíme odpovedajúcimi krivkami. V našom prípade vyvolajú normálové sily iba osamelé sily Ra,x a Fx, teda obrazec bude po častiach konštantný. |
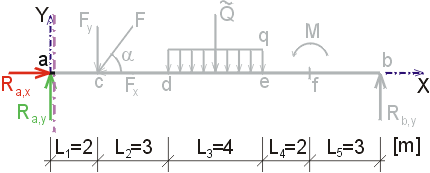 |
Va - vedieme rez v bode a tesne sprava.
Na odrezanej časti pôsobí v smere osi y iba reakcia Ra,y.
Podľa konvencie kladných posúvajúcich síl pôsobí v smere kladnom.
Teda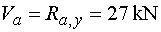 |
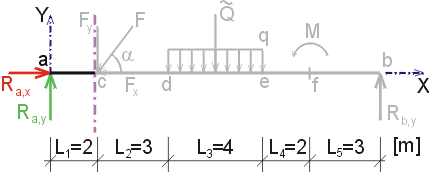 |
Vcl - vedieme rez v bode c tesne zľava.
To znamená, že na odrezanej časti nosníka nepôsobí eště sila F.
V smere osi y teda pôsobí stále iba reakcia Ra,y
(kladne). Teda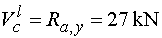 |
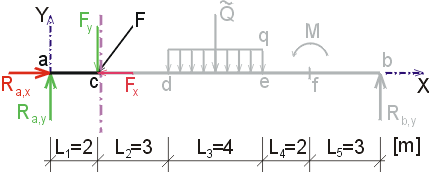 |
Vcp - vedieme rez v bode c tesne sprava.
To znamená, že na odrezanej časti nosníka už pôsobí aj sila F.
V smere osi y potom pôsobí reakcia Ra,y (kladne)
a zvislá zložka Fy sily F, pôsobiaca proti kladnej konvencii posúvajúcich síl, tj. záporne.
Teda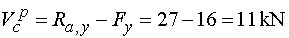 |
 |
Vdl - vedieme rez v bode d tesne zľava.
Na odrezanej časti nosníka pôsobí v smere osi y reakcia Ra,y (kladne) a zvislá zložka Fy (záporne).
Teda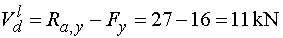 |
 |
Vdp - vedieme rez v bode d tesne sprava.
Na odrezanej časti nosníka začíná pôsobiť spojité rovnomerné zaťaženie.
Účinok tohto zaťaženie záleží na dĺžke pôsobenia. Ak sme v bode d, potom dĺžka pôsobenia zaťaženia na odrezanej časti
je nulová, a preto i účinok zaťaženia je nulový.
V smere osi y tak stále pôsobí iba reakcia Ra,y (kladne) a zvislá zložka Fy (záporne).
Teda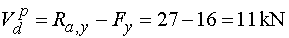 |
 |
Vel - vedieme rez v bode e tesne zľava.
V smere osi y na odrezanej časti nosníka pôsobí reakcia Ra,y (kladne), zvislá zložka Fy (záporne)
a celé spojité rovnomerné zaťaženie, ktoré je nahradené náhradným bremenom Q (prepokladáme nulovú vzdálenosť rezu
od bodu e).
Toto náhradné bremeno vyvolává taktiež zápornú posúvajúcu silu.
Teda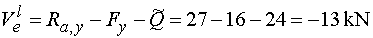 |
 |
Vep - vedieme rez v bode e tesne sprava.
V smere osi y na odrezanej časti nosníka pôsobí reakcia Ra,y (kladne),
zvislá zložka Fy (záporne) a celé spojité rovnomerné zaťaženie, ktoré je už nahradené náhradným bremenom
Q pôsobiaca záporne. Teda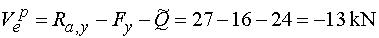 |
  |
Vfl, Vfp
- ak vedieme rez v bode f tesne zľava alebo tesne sprava (teda pred miestom pôsobenia osamrlého momentu
a za týmto miestom), vidíme, že na odrezanej časti nosníka nepribudne oproti rezu v bode e žiadne dalšie
zaťaženie v smere osi y, ktoré by vyvolalo zmenu posúvajúcej sily.
Na ľavú časť nosníka tak stále pôsobí iba reakcia Ra,y (kladne), zvislá zložka Fy (záporne)
a spojité rovnomerné zaťaženie, už nahradené náhradným bremenom Q (záporne).
Teda Vfl = Vfp
= Vf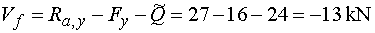 |
 |
Vb - ak určujeme posúvajúcu silu v bode b, vedieme rez tesne zľava.
Na odrezanej časti stále pôsobí v smere osi y reakcia Ra,y (kladne), zvislá zložka Fy (záporne)
a náhradné bremeno Q (záporne). Teda 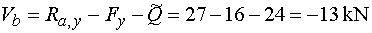 |
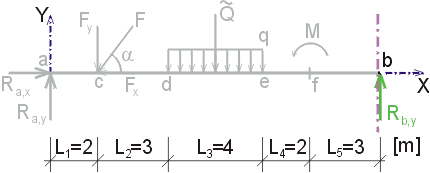 |
Vb - vedieme rez v bode b tesne zľava.
Na odrezanej časti pôsobí v smere osi y reakcia Rb, ktorá podľa konvencie vyvolává zápornú posúvajúcu sílu.
Teda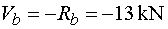 |
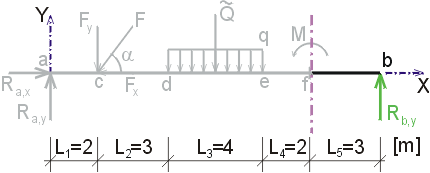 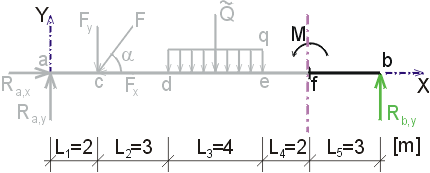 |
Vfp, Vfl
- ak vedieme rez v bode f tesne sprava alebo tesne zľava, zistíme, že na odrezanej časti pôsobí v smere
osi y v obidvoch prípadoch iba reakcia Rb (záporne).
Teda Vfp = Vfl
= Vf 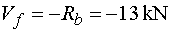 |
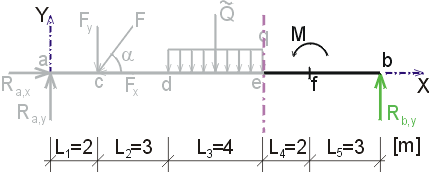 |
Vep - vedieme rez v bode e tesne sprava.
Na odrezanej časti pôsobí v smere osi y iba reakcia Rb (záporne). Teda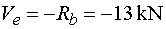 |
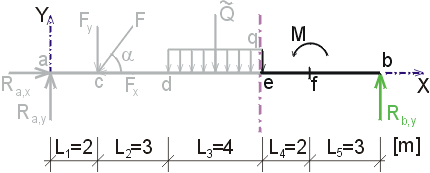 |
Vel - vedieme rez v bode e tesne zľava.
Na odrezanej časti pôsobí ve smere osi y reakcia Rb (záporne)
a dďalej začíná pôsobiť spojité zaťaženie. Dĺžka pôsobenia tohto zaťaženie na odrezanej časti je však nulová a teda aj účinok
zaťaženia je nulový. Teda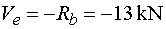 |
 |
Vdp - vedieme rez v bode d tesne sprava.
Na odrezanej časti pôsobí v smere osi y reakcia Rb (záporne) a celé spojité rovnomerné
zaťaženie (za predpokladu nulovej vzdialenosti bodu d od miesta rezu), ktoré je už nahradené náhradným bremenom Q,
ktoré vyvolá kladnú posúvajúcu silu.
Teda platí 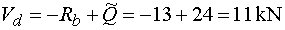 |
 |
Vdl - vedieme rez v bode d tesne zľava.
Na odrezanej časti pôsobí v smere osi y reakcia Rb (záporne) a celé spojité rovnomerné
zaťaženie, už nahradené náhradným bremenom Q, vyvolávajúcim kladnú posúvajúcu silu. Teda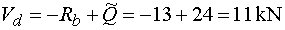 |
 |
r
Vcp - vedieme rez v bode c tesne sprava, t.j. tesne pred pôsobiskom sily F.
Na odrezanej časti pôsobí v smere osi y reakcia Rb (záporne) a náhradné bremeno Q (kladne).
Teda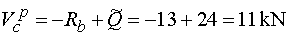 |
 |
Vcl - vedieme rez v bode c tesne zľava, t.j. tesne za pôsobiskom sily F.
Na odrezanej časti teraz pôsobí v smere osi y, okrem reakcie Rb (záporne) a náhradného bremena
Q (kladne) tiež zvislá zložka Fy, pôsobiaca taktiež kladne. Teda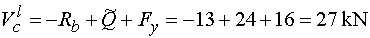 |
 |
Va - vedieme rez v bode a tesne sprava.
Na odrezanej časti pôsobí v smere osi y reakcia Rb (záporne), náhradné bremeno Q (kladne)
a zvislá zložka Fy (kladne). Teda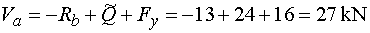 |
|
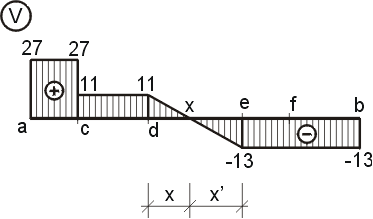
Ak máme vypočítané hodnoty posúvajúcich síl, môžeme nakreslit tzv. obrazec posúvajúcich síl (graf posúvajúcich síl,
priebeh posúvajúcich síl). Ten vykreslíme tak, že na os nosníka vynesieme vypočítané hodnoty. Kladné hodnoty posúvajúcich sil
vynášíme nad os nosníka, záporné pod os nosníka. Vynesené body potom spojíme odpovedajúcimi krivkami. Medzi bodmi a,c a
c,d bude priebeh konštantný, medzi bodmi d,e bude priebeh lineárny, pretože medzi bodmi pôsobí rovnomerné
spojité zaťaženie, a medzi bodmi e,f,b bude priebeh opäť konštantný. Z obrazca vidíme, že medzi bodmi e,d pretíná graf os nosníka (os x). Takémuto miestu hovoríme "nebezpečný" prierez, pretože v tomto mieste vzniká medzi bodmi d,e maximálny ohybový moment. Musíme teda presně určiť (lokalizovať) toto miesto x. |
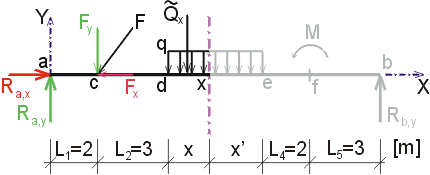
|
Určenie hodnoty x zľava ak vedieme rez medzi bodmi d,e v mieste x, tak posúvajúce sily vyvodia reakciu Ra,y, zložka Fy a časť spojitého zaťaženia q pôsobiaceho na dĺžke x. Náhradné bremeno Qx má veľkosť Qx=q.x. Potom pre veľkosť posúvajúcej sily platí : 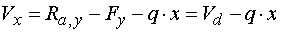 My však hľadáme také x, pre ktoré platí 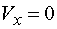 , teda hľadáme riešenie rovnice v tvare 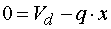 Riešením tohto vzťahu dostávame vzťah pre hľadanú hodnotu x : 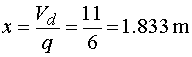 |
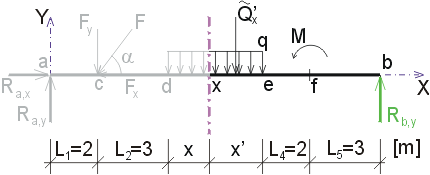
|
Určenie hodnoty x' sprava ak vedieme rez medzi bodmi d,e v mieste x, tak posúvajúce sily vyvodia reakciu Rb a časť spojitého zaťaženie q pôsobiaceho na dĺžke x'. Náhradné bremeno Q'x má veľkosť Q'x = q.x'. Potom pre veľkosť posúvajúcej sily platí : 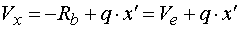 My hľadáme také x', pre ktoré platí 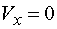 teda hľadáme riešenie rovnice 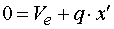 Riešením tohto vzťahu dostáváme vzťah pre hľadanú hodnotu x' : 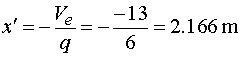 |
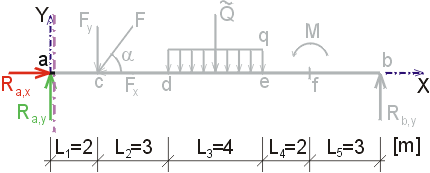 |
Ma - vedieme rez v bode a tesne sprava.
Na odrezanej časti pôsobí reakcia Ra,x a Ra,y. Zložka Ra,x
nevyvodí moment k bodu rezu, pretože nositeľka reakcie prechádza rezom. Zložka Ra,y precháza bodem a,
takže tiež nedokáže vyvodiť moment k rezu (prepokladáme, že vzdialenosť bodu a od rezu je nulová).
Teda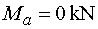 |
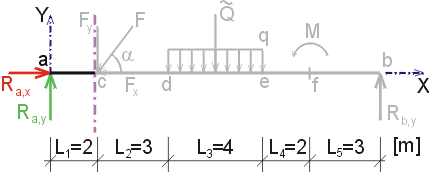 |
Mcl - vedieme rez v bode c tesne zľava. Znamená to, že na odrezanej časti nosníka
nepôsobí ešte sila F. Na odrezanej časti pôsobí reakcia Ra,x a Ra,y.
Zložka Ra,x nevyvodí moment k bodu rezu, pretože nositeľka reakcie opäť prochádza rezom (nositeľka prechádza
všetkými bodmi nosníka, takže v žiadnom reze nevyvodí momentový účinok).
Zložka Ra,y pôsobí na ramene L1 a teda vyvodí moment, který bude otáčať okolo bodu c
podľe konvencie kladne (teda bude ťahať dolné vlákna). Teda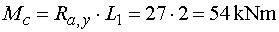 |
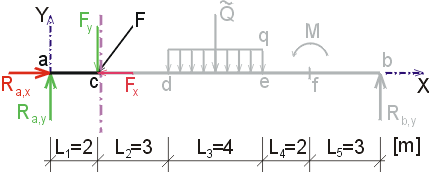 |
Mcp - vedieme rez v bode c tesne sprava.Na odrezanej časti nosníka už pôsobí aj sila
F. Z odrezanej časti vyvodí moment iba reakcia Ra,y na ramene L1
otáčejúca kladne.
Zložka Fx rovnako ako reakcia Ra,x nevyvodí moment, pretože prechádza bodom rezu.
Zložka Fy pôsobí v bode c a za predpokladu, že vzdialenosť miesta rezu od bodu c
je nulová, nevyvodí ani zložka Fy žiadny momentový účinok k bodu c.
Teda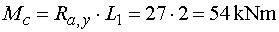 |
 |
Mdl - vedieme rez v bode d tesne zľava.
Z odrezanej časti nosníka vyvodí moment reakcia Ra,y a zložka Fy.
Reakcia Ra,y pôsobí na ramene (L1+L2) a okolo bodu
d otača kladne (ťahá dolné vlákna).
Zložka Fy pôsobí na ramene L2 a okolo bodu d otača proti kladnej
konvenci, tj. záporne (tlačí dolné vlákna).
Výsledný ohybový moment v reze je 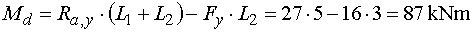 |
 |
Mdp - vedieme rez v bode d tesne sprava.
Na odrezanej časti nosníka začíná pôsobiť spojité rovnomerné zaťaženie. Účinok tohto zaťaženia záleží na dĺžke pôsobenia.
Ak sme v bode d, potom dĺžka pôsobenia zaťaženia na odrezanej časti je nulová, a preto aj účinok zaťaženia je nulový
(nevyvodí moment rovnako ako nevyvodí posúvajúcu silu).
Z odrezanej časti nosníka vyvodí moment opäť iba reakcia Ra,y a zložka Fy ako v
predchádzajúcom reze. Obidve sily pôsobia tiež na rovnakých ramenách a otáčajú rovnakým smerom, takže platí rovnaký vzťah :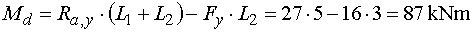 |
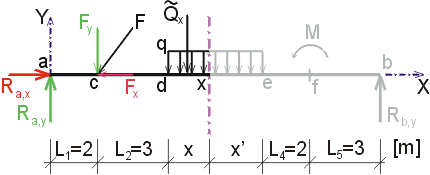 |
Mx - pretože sme pri výpočte posúvajúcich síl našli nebezpečný prierez, musíme v tomto reze určiť veľkosť momentu.
Veďme teda rez v bode x.
Z odrezanej časti nosníka vyvodí moment reakcia Ra,y,zložka Fy a náhradné bremeno Qx,
ktoré nahradzuje časť spojitého zaťaženia pôsobiaceho na odrezanej časti.
Reakcia Ra,y pôsobí na ramene (L1+ L2+x) a otáča kladne.
zložka Fy pôsobí na rameni (L2+ x) a otáča záporne. Náhradné bremeno Qx
pôsobí na ramene x/2 a otáča tiež záporne. Výsledný ohybový moment v rezu potom je 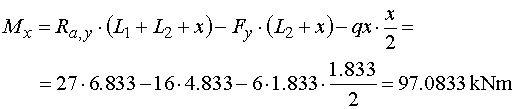 |
 |
Mel - vedieme rez v bode e tesne zľava.
Z odrezanej časti nosníka vyvodí momentový účinok iba reakcia Ra,y, zložka Fy a
náhradné bremeno Q (předpokládáme, že vzdialenosť rezu k bodu e je nulová).
Reakcia Ra,y pôsobí na ramene (L1+
L2+L3) a okolom bodu e otača podľa konvencie kladne (ťahá dolné vlákna).
Zložka Fy pôsobí na ramene (L2+
L3) a okolo bodu e otáča podľa konvencie záporne (tlačí do dolných vlákien).
Náhradné bremeno Q pôsobí na ramene L3 /2 a okolo bodu e otáča podľa konvencie záporne
(tlačí dolní vlákna). Výsledný ohybový moment v rezu potom je 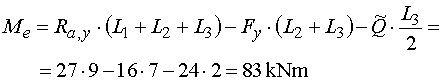 |
 |
Mep - vedieme rez v bode e tesne sprava.
Z odrezanej časti nosníka vyvodí moment opäť reakcia Ra,y, zložka Fy a náhradné
bremeno Q.
Všetky sily pôsobia na rovnakých ramenách a otáčajú rovnakým smerom ako v predchádzajúcom reze. Platí teda rovnaký vzťah :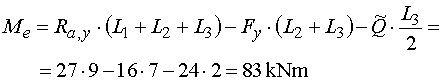 |
 |
Mfl - vedieme rez v bode f tesne zľava (teda pred miestom pôsobenia osamelého momentu).
Z odrezanej časti nosníka vyvodí moment opäť iba reakcia Ra,y, zložka Fy a náhradné
bremeno Q.
Všetky sily otáčajú okolo bodu f rovnakým smerom ako v predchádzajúcich dvoch rezoch (majú teda rovnaké znamienka), pôsobí však na iných ramenách.
Reakcia Ra,y na ramene (L1+L2+L3+L4)=
(L-L5), zložka Fy na ramene (L2+L3+L4)
a náhradné bremeno Q na ramene (L3 /2+L4).
Výsledný moment potom je : 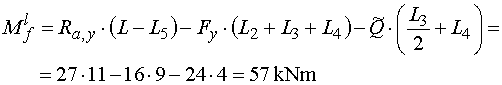 |
 |
Mfp - vedieme rez v bode f tesne sprava (teda za miestom pôsobenia osamelého momentu).
Z odrezanej časti nosníka vyvodí moment reakcia Ra,y, zložka Fy, náhradné bremeno Q a
osamělý moment M.
Všetky sily pôsobia na rovnakých ramenách a otáčajú okolo bodu f rovnakým smerom ako v predchádzajúcom reze.
Naviac tu pôsobí ešte moment M, ktorý otača podľae konvencie záporne.
Výsledný moment potom je :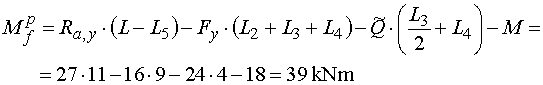 |
 |
Mb - ak určujeme ohybový moment v bode b, vedieme rez tesne zľava.
Z odrezanej časti vyvodí moment reakcia Ra,y na ramene L (otáčí kladne),
zložka Fy na ramene (L-L1) (záporne), náhradné bremeno
Q na ramene (L3 /2+L4+L5)
(záporne) a moment M (záporne).
Výsledný moment potom je :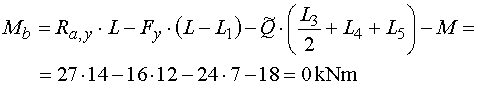 |
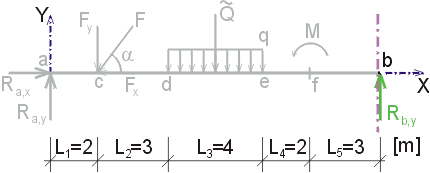 |
Mb - vedieme rez v bode b tesne zľava.
Na odrezanej časti pôsobí iba reakcia Rb, ktorá nevyvodí k miestu rezu moment, pretože predpokládáme, že
vzdialenosž rezu od bodu b je nulová.
Teda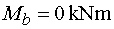 |
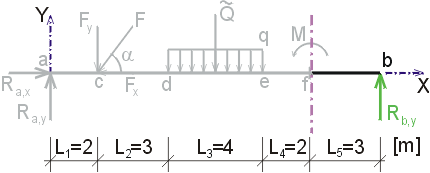 |
Mfp - vedieme rez v bode f
tesne sprava (teda pred miestom pôsobenia osamelého momentu).
Z odrezanej časti momentový účinok vyvodí iba reakcia Rb, pôsobiaca na ramene L5 a
otáčajúca podľa konvencie kladne.
Teda e 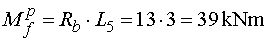 |
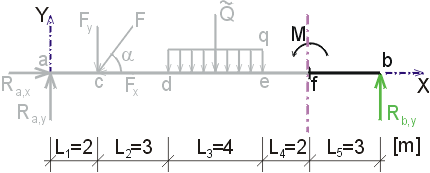 |
Mfp - vedieme rez v bode f tesne zľava (teda za miestom pôsobenia osamelého momentu).
Z odrezanej časti moment vyvodí iba reakcia Rb a osamelý moment M.
Reakcia Rb pôsobí na ramene L5 a otáča okolo bodu f podľa konvencie kladne. Osamělý moment M otáčí také kladne.
Teda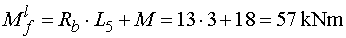 |
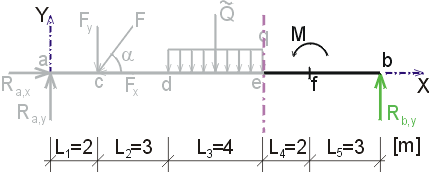 |
Mep - vedieme rez v bode e tesne sprava.
Z odrezanej časti vyvodí moment reakcia Rb a osamelý moment M. Reakcia Rb
pôsobí na ramene (L4 + L5) a otáča kladne. Moment taktiež otáča kladne.
Teda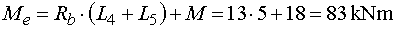 |
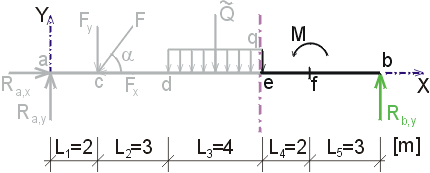 |
Mel - vedieme rez v bode e tesne zľava.
Na odrezanej časti nosníka začíná pôsobiť spojité rovnomerné zaťaženie.
Účinok tohto zaťaženia záleží na dĺžke pôsobenia. Ak sme v bode e,potom dĺžka pôsobenia zaťaženia na odrezanej časti je
nulová, a preto aj účinok zaťaženia je nulový (nevyvodí moment rovnako ako nevyvodí posúvajúcu silu).
Z odrezanej časti nosníka vyvodí moment iba reakcia Rb a osamelý moment M na rovnakých ramenách
ako v predchádzajúcom reze.
Platí preto rovnaký vzťah :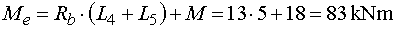 |
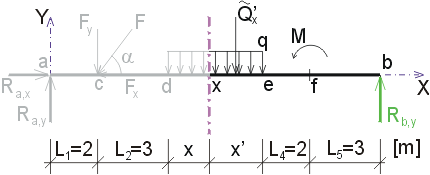 |
Mx - pretože sme pri výpočte posúvajúcich síl našli aj nebezpečný prierez, musíme v reze cez neho určiť aj
veľkosť momentu v ňom.
Vedieme teda rez v bode x. Z odrezanej časti nosníka vyvodí moment iba reakcia Rb,
osamelý moment M a náhradné bremeno Q'x,ktoré nahrádza časť spojitého zaťaženia pôsobiaceho na
odrezanej časti.
Reakcia Rb pôsobí na ramene (x'+L4+L5) a otáča kladne.
Osamelý moment otáča tiež kladne a náhradné bremeno Q'x pôsobí na ramene x'/2 a otáča záporne.
Výsledný ohybový moment v rezu potom je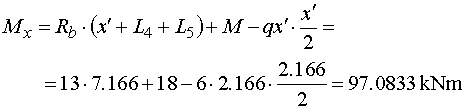 |
 |
Mdp - vedieme rez v bode d tesne sprava.
Z odrezanej časti vyvodí moment k miestu rezu reakcia Rb, osamělý moment M a náhradné bremeno Q
(predpokladáme, že vzdialenosť rezu k bodu e je nulová).
Reakcia Rb pôsobí na ramene (L3+L4+L5) a otáča kladne.
Osamelý moment M tiež otáča kladne a náhradné bremeno Q pôsobí na ramene (L3 /2) a otáča proti konvenci,
teda záporne. Pre výsledný ohybový moment potom platí :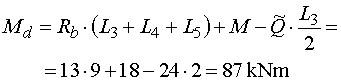 |
 |
Mdp - vedieme rez v bode d tesne zľava.
Z odrezanej časti vyvodí moment k miestu rezu reakceia Rb, osamělý moment M a náhradné bremeno Q.
Obidve sily a moment pôsobia na rovnakých ramenách a otáčajú rovnakým smerom ako v predchádzajúcom reze. Takže platí rovnaký vzťah :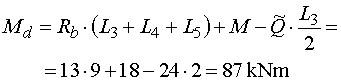 |
 |
Mcp - vedieme rez v bode c tesne sprava.
To znamená, že na odrezanej časti nosníka nepôsobí eště sila F. Z odrezanej časti vyvodí moment k miestu rezu iba reakcia Rb,
osamelý moment M a náhradné břemeno Q.
Reakcia Rb pôsobí na ramene (L-L1) a otáča kladne. Osamelý moment M tiež otáča kladne a
náhradné bremeno Q pôsobí na ramene (L2+L3 /2) a otáča záporne.
Pre výsledný ohybový moment platí vzťah: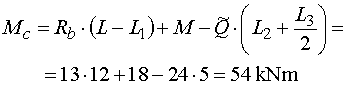 |
 |
Mcl - vedieme rez v bode c tesne zľava.
To znamená, že na odrezanej časti nosníka už pôsobí aj sila F. Jej zložky Fx a Fy ale nevyvodia k miestu
rezu moment, nakoľko zložka Fx prechádza bodom c a zložka Fy pôsobí na nulovom ramene.
Moment k miestu rezu teda vyvodí iba reakcia Rb, osamelý moment M a náhradné bremeno Q. Obidve sily aj moment pôsobia
na rovnakých ramenách a otáčajú rovnakým smerom ako v predchádzajúcom prípade, preto platí rovnaký vzťah :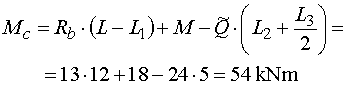 |
 |
Ma - vedieme rez v bode a tesne sprava.
Z odrezanej časti vyvodí moment reakcia Rb, osamelý moment M, náhradné bremeno Q a zložka Fy.
Reakcia Rb pôsobí na ramene L a otáčí kladne, osamelý moment M otáča tiež kladne, náhradné bremeno Q
pôsobí na ramene (L1+L2+L3 /2) a otáča záporne a zložka Fy pôsobí
na ramene L1 a otáča tiež záporne. Pre výsledný moment platí teda vzťah :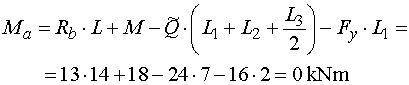 |
|
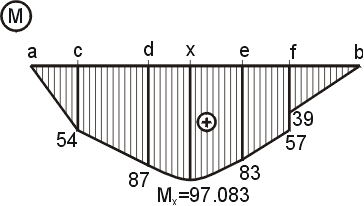
Ak máme vypočítané hodnoty ohybových momentov, môžeme vykreslit tzv. obrazec ohybových momentov (graf ohybových momentov, priebeh ohybových momentov). Ten vykreslíme tak, že na os nosníka vynesieme vypočítané hodnoty. POZOR ! Kladné hodnoty ohybových momentov vynášame pod os nosníka, záporné nad os nosníka. Vynesené body potom spojíme odpovedajúcimi krivkami. Medzi bodmi a,c a c,d bude priebeh lineárny, medzi bodmi d,e bude priebeh parabolický, pretože na tomto údeku pôsobí rovnomerné spojité zaťaženie, a medzi bodmi e,f,b bude priebeh opät lineárny. |
Prostý nosník - ilustračný príklad - bez podrobného popisu
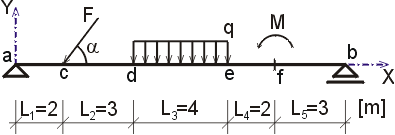
|
Určte reakcie a priebehy vnútorných síl na zadanom prostom nosníku. F = 20 kN, cosa = 0.6, sina = 0.8, q = 6 kN/m, M = 18 kNm. |
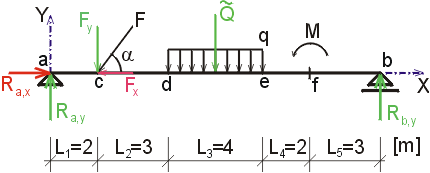 |
1) Výpočet reakciíRozloženie sily F :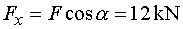 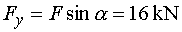 Nahradenie spojitého rovnomerného zaťaženia q : 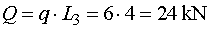 Zakreslenie zložiek reakcií. Podmienky rovnováhy : 1) 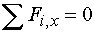 : :
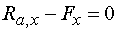 2) 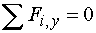 : :
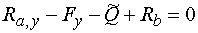 3) 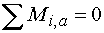 : :
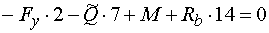 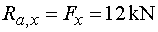 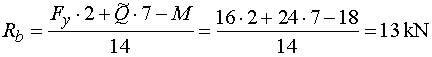 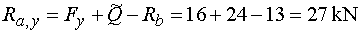 |
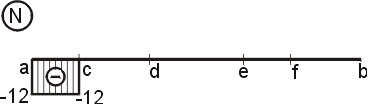 |
2) Výpočet vnútorných sílNormálové sily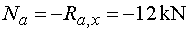 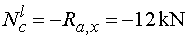 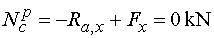 |
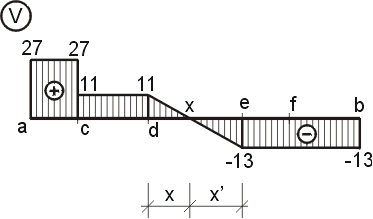 |
Posúvajúce sily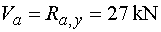 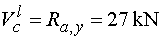 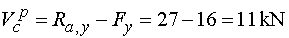 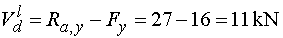 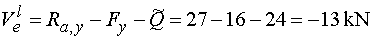 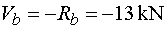 Nebezpečný prierez : 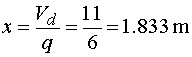 |
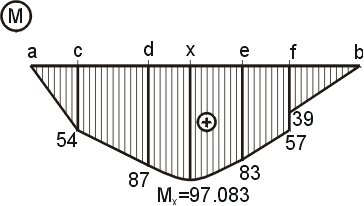 |
Ohybové momenty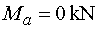 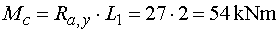 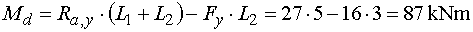 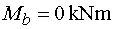 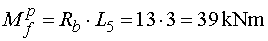 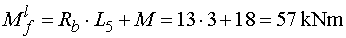 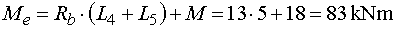 Maximálny moment v nebezpečnom priereze x : 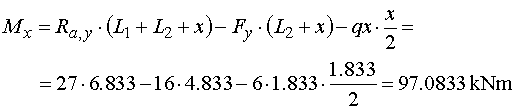 |